Sur la rédaction de
L'Univers égale un

Toute sa vie, André Deslongchamps veut savoir l’absolu. Rêveur, il se questionne sur l’Univers. À l’université, ce n’est pas d’apprendre les notions de génie qui l’intéressent, mais de trouver réponse à ses questions, toutes du côté de l’insondable, de l’impénétrable : gravitation, lumière, électromagnétisme, relativité, matière, astres, vie, phénomènes inexpliqués. Sa quête se résume à où, quand, comment, pourquoi et qui. À vingt ans, à trente ans, à quarante ans…, ses livres de chevet demeurent les livres d’école. Peut-on y percer le mystère à leur relecture, s’obstine-t-il à croire? Il veut comprendre.
Puis, été 2001, lisant à la file deux best-sellers sur la physique, André a une idée. Il croit avoir décelé la structure de la matière, des quarks, et il veut communiquer sa trouvaille. Débute alors la rédaction de L’Univers égale un, bouquin de vulgarisation, grand public.
Or, vulgarisation signifie récapitulation des notions de base en physique. Mais voilà qu’en voulant expliquer la Relativité d’Einstein autrement qu’en développant uniquement des formules, jaillit une seconde idée. Espace et temps ne sont pas des variables fondamentales, la vitesse en étant dérivée, mais bien l’inverse : espace et temps sont des variables dérivées, dans le rapport inextricable 300 000 km/s, alors que la vitesse est une variable fondamentale, celle de la lumière en étant l’unité.
S’amorce une approche graphique où tout est centré sur l’observateur O, où tout est relié à la vitesse v, fraction de c, d’une entité P en mouvement par rapport à O. L’espace se déploie devant O et le temps se déploie perpendiculairement à l’espace, partant de O. Surtout, le rapport d’échelle dans le graphique entre espace et temps doit égaler 1, soit que 300 000 kilomètres = 1 seconde = 1 unité d’échelle = distance unitaire entre deux bornes d’espace = distance unitaire entre deux bornes de temps, alors que c = 1. Autrement dit, une unité d’espace égale une unité de temps et leur rapport (vitesse) donne un, soit c égale un. Il suffit ensuite de tracer un cercle de rayon un, centré en O, pour remarquer que la tangente à ce cercle, perpendiculairement à l’axe du temps, est le lieu des vitesses, accessoirement du rapport v/c. Du coup, André trouve les lieux des facteurs d’Einstein de contraction de l’espace et de dilatation du temps, γ = 1/α = 1/(1 – v2/c2)1/2, bien à l’échelle dans le graphique, α émergeant en cosinus et γ en sécante. Tout déboule ensuite, bien inscrit dans ce cercle : transformations de Lorentz, addition des vitesses selon Einstein, lieux du travail, de l’énergie, de l’impulsion, du momentum, de la masse, du photon, du neutrino…, chaque entité étant à l’échelle et en relation graphique absolue avec les autres, en tout respect des formules physiques. Ce cercle devient cercle trigonométrique relativiste, ou CTR. En particulier, André étudie les paraboles d = ½at2, de la distance classique franchie en fonction du temps qui s’écoule, alors que P est accéléré uniformément. Il en extrait le lieu de l’accélération dans le CTR et, conséquemment, celui des forces gravitationnelle, électromagnétique. La figure 1 montre où se situent les facteurs α et γ dans le cercle trigonométrique relativiste.
Selon Pythagore, dans le triangle OO’A :
(OO’)2 + (O’A)2 = (OA)2 → (v/c)2 + α2 = 1
→ α = √(1 – v2/c2).
α étant cosinus, OS en est sécante γ
→ γ = 1/α = 1/√(1 – v2/c2).
OV est une courbe de
distance OO’ franchie en un temps OT,
alors que la vitesse d’O’ est constante,
valant v, fraction de c,
donnant ici pente VT/OT,
indiquée sur l’axe de vitesse,
tangente au cercle.
note : O’ s’éloigne d’O.
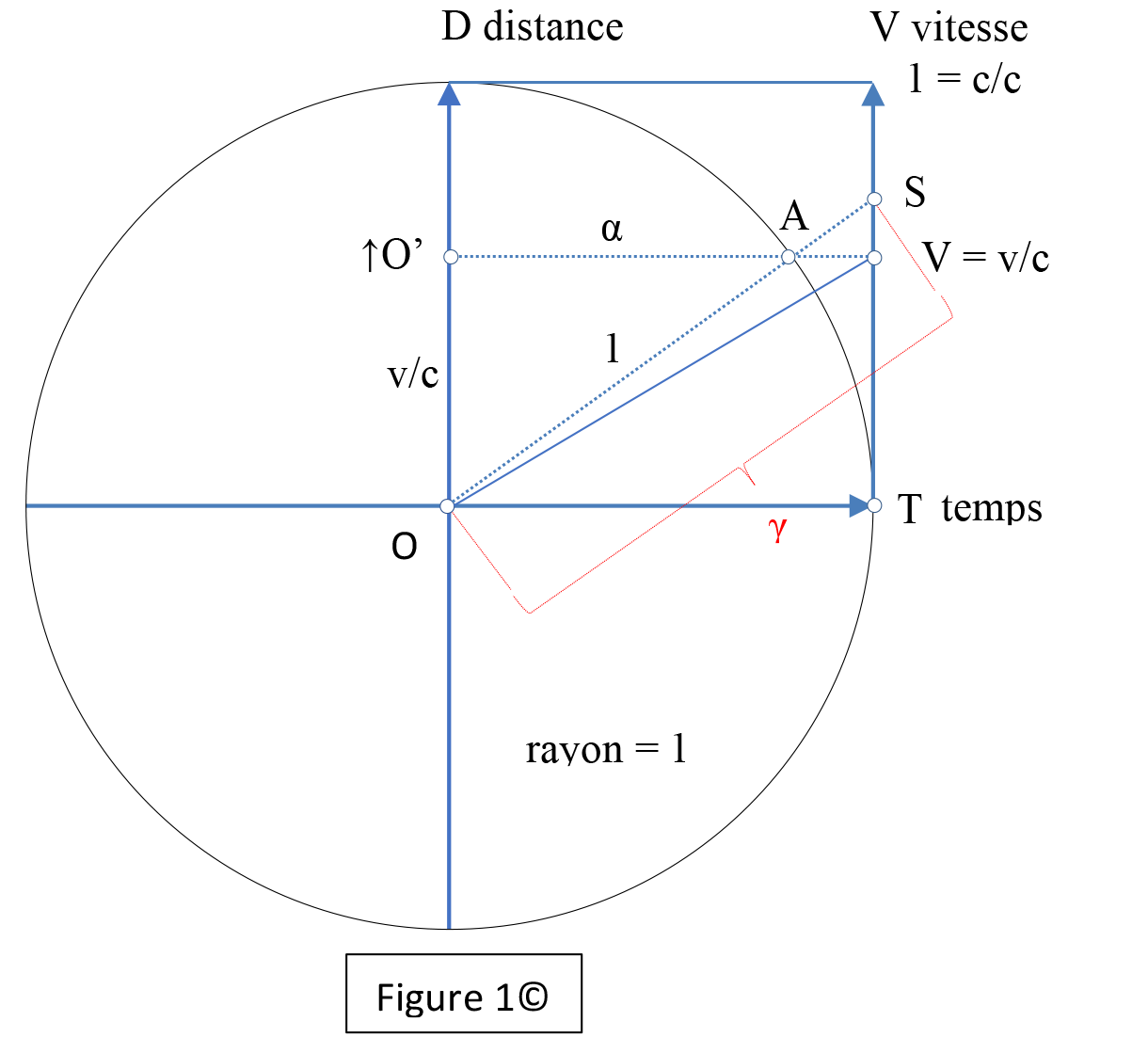
Si OT est l’unité de temps de O, disons 1 secondeO,
OS devient celle de O’, soit 1 secondeO’,
avec OS dilatée du facteur γ par rapport à OT
En physique, les variables de base sont de formulation simple : v = d/t, a = v/t, d = ½at2, p = mv, F = ma, E = ½mv2, T = Fd = ΔE, I = Ft = Δp, c = νλ, E = mc2, E = hν… toutes issues d’une multiplication, d’une division, d’une élévation au carré, d’un rapport inverse ou d’un rapport inverse au carré, à l’image des fonctions linéaire y = mx, quadratique y = mx2, racine carrée y = √(x/m), inverse y = 1/x et quadratique inverse y = m/x2, auxquelles s’ajoutent logarithmique y = ln(x) et exponentielle y = ex. Notons que c’est la fonction y = 1/x qui mène à ln(x) et à ex, permettant d’y voir ee et les formules unitaires donnant 1 kg2/C2, 1 A, 1 kg2/C2/A et 1 Js3. Trouver les lieux de ces variables dans le cercle trigonométrique relativiste, c’est mettre en relief ces fonctions mathématiques.
En particulier, trouver le lieu de l’accélération – et celui des forces, conséquemment – demande l’analyse de la formule d = ½at2 = mx2, cas le plus simple de variation de distance franchie en fonction du temps qui s’écoule, d’une particule P ayant quitté (d0 = 0) un observateur O avec une vitesse initiale nulle (v0 = 0), alors que son accélération par rapport à O est constante, valant a. Sans aller dans le détail de la démonstration donnée dans le livre, identifiant ce fameux lieu, un coup d’œil à la figure 2 en donne l’amorce. La figure 3 affiche, non pas le lieu final de a, mais la valeur 1/a issue de d = ½at2 et l’oblique verte y = ½x servant à la localiser.
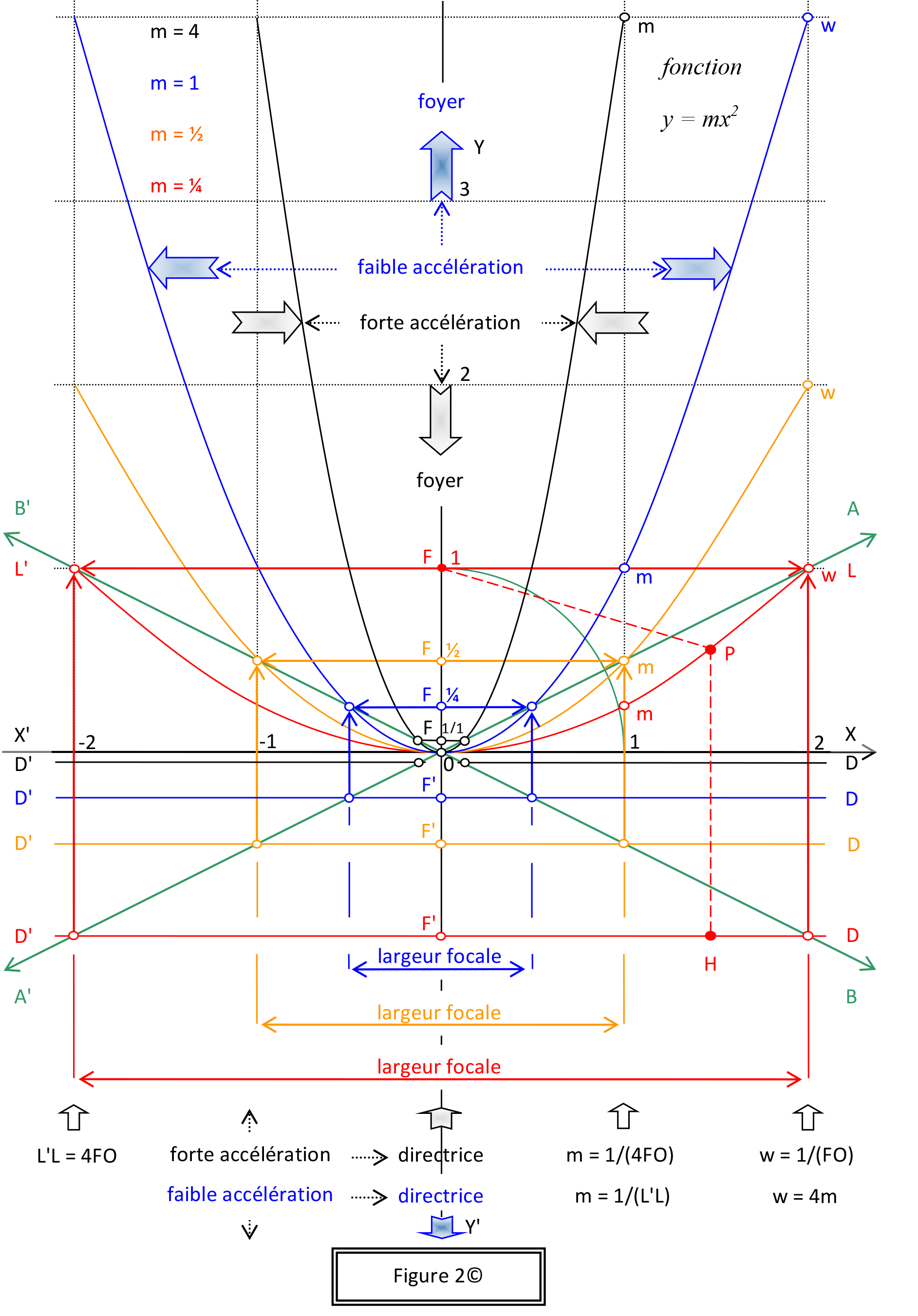
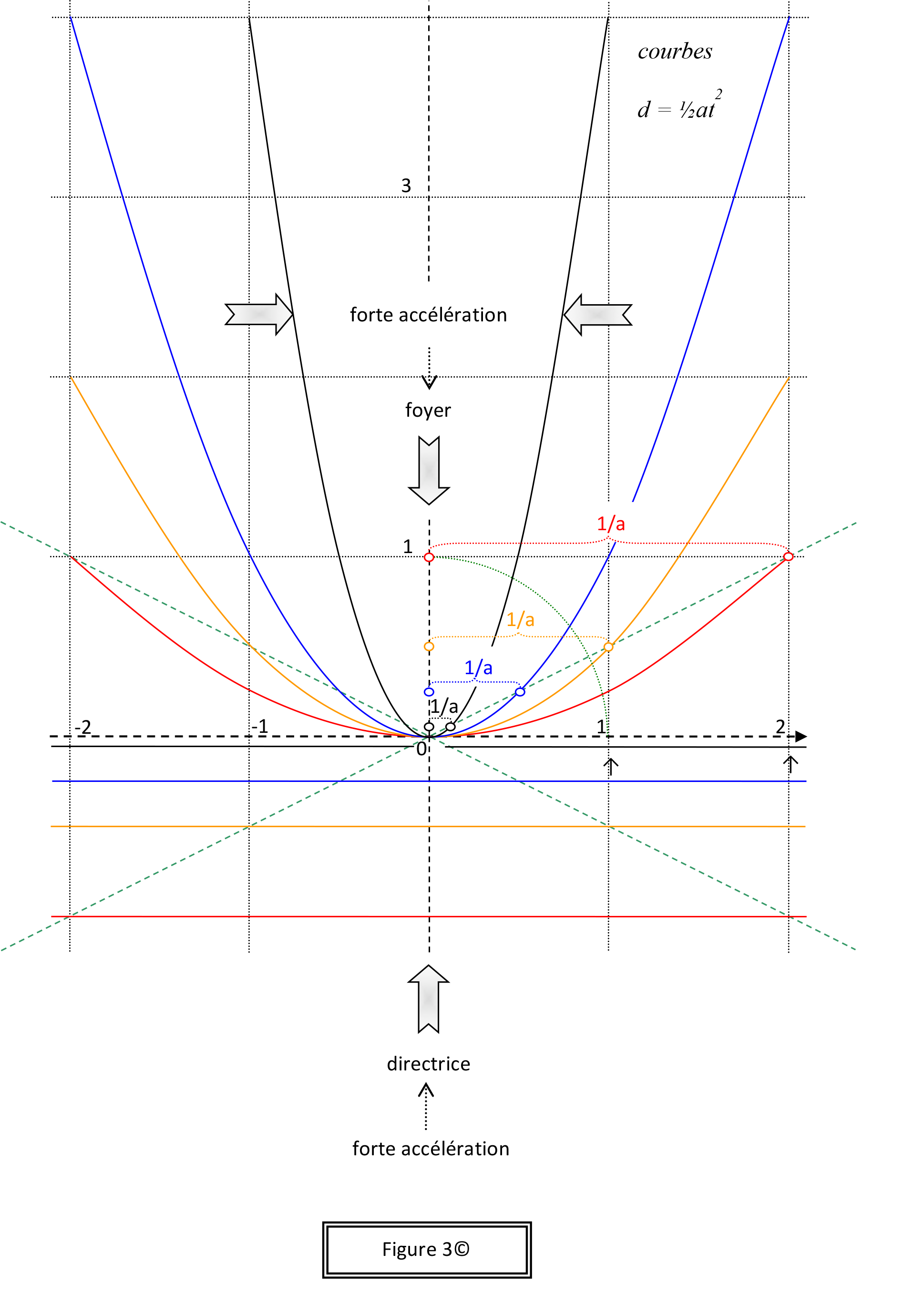
Troisième idée, en voulant expliquer le mouvement à vitesse constante d’une entité P par rapport à un observateur O, André remarque que seul un observateur O’ en colinéarité avec O et P peut aussi conclure que P se déplace à vitesse constante par rapport à lui. Pour tout autre observateur O’’ non en colinéarité avec O et P, il n’y a pas constat de vitesse constante de P. Cas particulier, si P est un photon et que la lumière file toujours à vitesse constante c pour tous, comment dénouer l’impasse? Le photon emprunte un trajet hyperbolique, où O et O’’ servent de foyers. Et cette solution nous fait comprendre forces gravitationnelle et électromagnétique. La figure 4 amorce la discussion… à poursuivre dans le livre.

O’ est au repos par rapport à O et O, O’ et P sont colinéaires.
O et O’’ sont au repos l’un par rapport à l’autre, distants d’un mètre. Partant d’O, P s’éloigne de lui à la vitesse constante de 1 m/s, de borne en borne, le long de la ligne de visée OP.
Par contre, selon ses lignes de visée, O’’ voit P s’éloigner de lui à vitesse variable puisque, de seconde en seconde, de borne en borne, P franchit tour à tour √2 m, puis √5 m, puis √10 m…, en utilisant la formule de Pythagore dans les triangles O’’OA, O’’OB, O’’OC…
Sur un autre plan, certains physiciens cherchent, oui, depuis cent ans, à unifier les constantes fondamentales en une formule qui égale 1, alors que les autres crient foutaise! Et André de jongler avec ces constantes et d’avoir une quatrième idée. Ce qui relie ces constantes, c’est le nombre ee, lequel est aussi inscrit dans le CTR via la courbe 1/x. En particulier, en utilisant les données CODATA 2010, ce facteur permet de fixer exactement la valeur de la constante de gravitation à G = 6,672 238 885 x 10–11 Nm2/kg2, ainsi que de ramener le rayon de l’électron à re = 0,8499810667 x 10–22 m.
L’Univers égale un contient plein d’autres sujets, lesquels ne peuvent pas tous être abordés dans cette présentation sommaire. Par exemple, dans une démarche non ad hoc, sachez qu’on y redéfinit les limites de l’infiniment petit, très proches des unités de Planck, sans être exactement les mêmes, et qu’on y explique la stabilité du proton, intimement liée à l’horizon de l’Univers, via une formule unitaire valant encore 1 Js3, liant constante de Planck (infiniment petit), âge de l’Univers (infiniment grand) et ratio masse du proton sur masse de l’électron (mp/me). Autre exemple, dans L’Univers égale un, nul besoin d’un univers à quatre dimensions – trois d’espace, une de temps –, parce que le temps est déjà dans l’espace, puisque l’espace-temps de l’observateur O est bidimensionnel, DT, dans le cercle trigonométrique relativiste, en rotation de 45◦ dans un plan bidimensionnel strictement spatial, XY. Au final, la troisième dimension spatiale, Z, sert d’axe de rotation dudit cercle, donnant en particulier la figure 5.
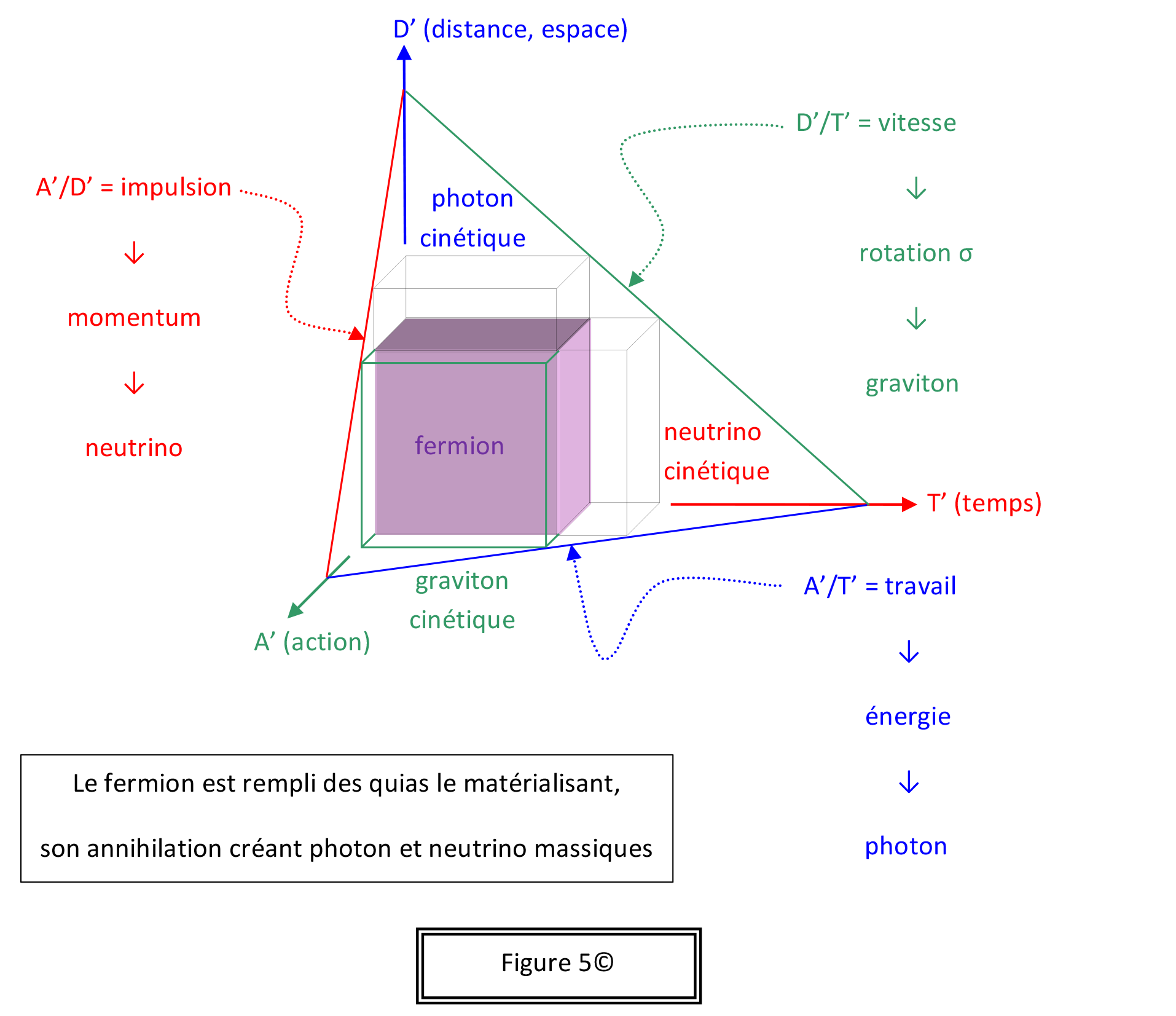
Dans L’Univers égale un, André convient de cent douze énoncés pour modéliser l’Univers. Ceux-ci sont énumérés dans la table des matières ci-après. Au chapitre 10, il ébauche en trente-neuf scènes un scénario de l’Univers.
Dans L’Univers égale un, il n’y a plus quatre variables fondamentales indépendantes, distance, temps, masse et charge électrique, piliers de la physique, mais deux seulement, vitesse et charge électrique massique. La valeur unitaire de la vitesse est celle de la lumière, soit c, et celle de la charge électrique massique est celle du quia, soit e±/me. Distance et temps sont inextricables du rapport c. Charge électrique et masse sont inextricables du rapport e±/me.
Dans L’Univers égale un, il n’y a qu’un axiome, celui avancé par Einstein, à l’effet que la lumière se déplace à vitesse constante c pour tous les observateurs qui en font la mesure, que ceux-ci soient au repos ou en mouvement relatif, constant ou variable. Tout le reste se déduit de cet axiome. La lumière est la clé de tout.
André vous souhaite bonne lecture.
