Sur l'idée initiale de
L'Univers égale un

Quels best-sellers l’auteur a-t-il lu, le menant à la rédaction de L’Univers égale un?
- Heinz Pagels, L’Univers quantique – Des quarks aux étoiles, InterÉditions, Paris 1985;
- Yuval Ne’eman, Yoram Kirsh, Les chasseurs de particules, Odile Jacob, Sciences, Paris, mars 1999.
Et quelle idée première – sa trouvaille, dit-il – voulait-il communiquer au lecteur?
En lisant ces bouquins, André se concentre sur la désintégration des baryons, des mésons et des leptons. Tout converge vers les résidus proton, électron, photon et neutrino. À l’intérieur des baryons et des mésons, les quarks ont un comportement bizarre. Ce sont eux qui semblent se désintégrer. Les quarks plus lourds disparaissent au profit de quarks plus légers. En plus, les quarks se désintègrent en se multipliant, de 3 quarks dans l’hadron initial, en 5 quarks, en 7 quarks, en 9 quarks…, au total, dans les produits de désintégration. Au premier coup d’œil, on peut même affirmer que les quarks sont constitués de mésons, notamment des pions. Or, les pions se décomposent eux-mêmes en électrons, photons et neutrinos. Conséquemment, André croit légitime d’affirmer que les quarks sont constitués d’électrons, contredisant les physiciens. À tout le moins, il voit comment c’est effectivement le cas, schématiquement.
André reprend toutes les désintégrations d’hadrons, soulignant la métamorphose à la chaîne des quarks et des produits de désintégration qui en résultent. Par exemple, la décomposition du baryon Ξb– (dsb) résulte en un baryon Ξb0 (usb) et en les résidus e– et νe, alors que celle du neutron n (udd) résulte en un proton p (uud) et en les mêmes résidus. C’est donc dire, dans ces cas, qu’il y a eu métamorphose du quark d en un quark u et éjection d’un électron et d’un antineutrino. Or, bien souvent, on voit plutôt un quark d se métamorphoser en un quark u en émettant un pion, comme dans le cas de la désintégration du baryon Σc0 (ddc) en Λc+ (udc) et π–, par exemple. Or, fait étrange, on voit autant l’inverse, c’est-à-dire un quark u se transformer en un quark d en émettant un pion, comme dans le cas de la désintégration du baryon Σc++ (uuc) en Λc+ (udc) et π+, par exemple. Mais alors, les quarks u et u, d et d, sont-ils différents ou sont-ils identiques? Sommes-nous en droit de conclure qu’il existe plusieurs variétés de quarks u et de quarks d, se demande-t-il?
Dans sa schématisation, André imagine les quarks être des filaments et leur décomposition être la fragmentation de ces filaments. En l’absence de données sur le quark t, il choisit la séquence de décomposition b → c → s → d → u en prenant soin d’y inclure les variantes c3, c2, c1, c0, s2, s1, s0, d2, d1, d0, u1 et u0. Pour se fixer une échelle, il choisit le quark u0 être deux fois la longueur d’un électron et le neutrino électronique (massique) être la longueur d’un électron. Après tout, la masse du quark u0 fait en moyenne quatre fois celle d’un électron. Il convient aussi que les pions et les kaons cachés dans les quarks sont eux-mêmes des filaments et qu’ils se décomposent selon le tableau 1.6 (c1) dans le livre. Il utilise donc ces propriétés filamenteuses pour trouver de la cohérence entre les quarks, l’idée étant de déterminer le bagage génétique des quarks supérieurs par rapport à celui du quark de base, c’est-à-dire u0. Sans l’ombre d’un doute, tous les quarks, ux, dx, sx, cx, bx, se réduisent donc génétiquement en quarks u0, en électrons et en neutrinos électroniques et en leurs équivalents d’antimatière, u0, e+ et νe. Au final, schématiquement, cette décomposition prend la forme d’un escalier régulier, la première (dernière) marche étant le quark u0, vraisemblablement indécomposable.
Puis, André convient d’un énoncé ad hoc, sur le coup. Ayant déjà statué qu’un filament u0 valait deux filaments e± dans ses schémas-escaliers, il affirme que le quark u0 est aussi constitué d’électrons, comme les autres, en toute conséquence. De combien d’électrons? Deux, pas plus : un positif, l’autre négatif, surnommés quias et notés ¶± pour simplifier le vocabulaire, l’écriture. Pourquoi? Cela confère à u0 une charge électrique nulle bien plus élégante que cet embêtant +⅔ et cela donne encore plus de cohérence à la schématisation des hadrons et à la création/annihilation de paires à l’interface du vide, celle e+/e– en l’occurrence, ce que les énoncés suivants dans le livre illustreront. En plus et surtout, au final, cela permet d’éliminer la notion de quark et de confondre matière et antimatière. En effet, si u0 = e+ + e–, alors, u0 = e– + e+ = u0. Donc la notion anti u0 = u0 devient inutile et celle d’antimatière aussi, accessoirement. Les hadrons étant désormais constitués uniquement d’électrons et de positrons, leurs charges électriques demeurent 0 ou ±1. Il est à noter que cette hypothèse à l’effet que les hadrons ne sont constitués que d’électrons, de positions, n’est pas nouvelle, qu’elle a été rejetée par les physiciens. L’approche est différente, cette fois-ci. Elle mène très loin, jusqu’à la plénitude du vide.
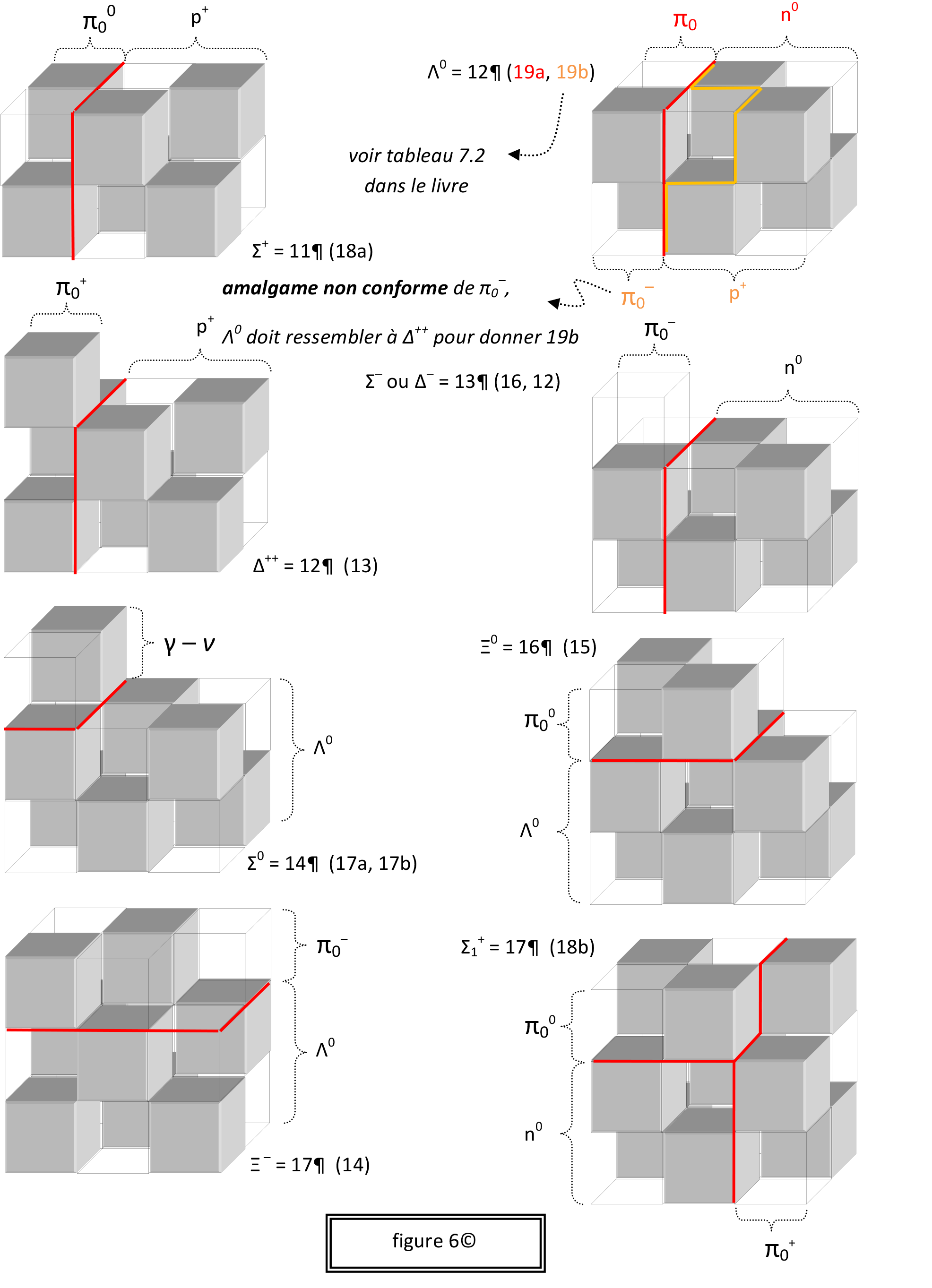
André dispose ses quarks filamenteux le long des axes d’espace XYZ dans le cas des baryons, XY dans celui des mésons, et X dans celui des leptons lourds, alors que l’électron lui-même s’apparente à un point, ou brique unitaire pour faire imagé. Cette amorce de structure de la matière fondamentale s’inspire de celle des minéraux à une échelle plus grande, comme si la nature n’avait qu’une configuration à nous proposer; le baryon tout en volume rappelant le diamant, le méson tout en surface rappelant le mica, le lepton tout en fil rappelant l’amiante et l’électron ponctuel rappelant la poussière. En donnant à chaque quark ux, dx, sx, cx, bx, une valeur m quias, chaque baryon contient n quias au total, disposés en point, ligne, surface, volume. Du coup, toute désintégration d’hadron saute aux yeux, via plans de clivage, délaissant surface ici, ligne là ou simple point. Plus loin dans le développement, les n quias d’un hadron deviendront ses quias de valence, alors que sa masse s’exprimera en p quias. Extraite du livre, la figure 6 met en image ce propos. Chaque cube est un quia (gris+, transparent–). Un pion π00 vaut 4¶, un pion π0– vaut 5¶, un proton p+ vaut 7¶, un neutron n0 vaut 8 ¶… et un Σ1+ vaut 17¶. Cette schématisation simple ne contrevient pas à la physique observée en laboratoire; elle l’illustre facilement pour la rendre compréhensible à toutes et à tous. En fin d’exercice, un neutron sera représenté par un cube parfait, rempli de quias en quantité suffisante pour y faire sa masse. Cette structure permettra de ranger sans vide en eux les neutrons dans une étoile à neutron, imageant la finalité de l’Univers… ou sa naissance.